Side Project: The Knights Tour - TS
2025-07-13
Preface
At our final examl in "algorythm's and datastrucures 1" we had to solve the "Knights tour" problem on paper.
It was a fun excersise, but ultimatly one i could not solve without sloppy extensions under the time constraints. So i wanted to look at it again and see what i could do.
The Knights tour
Placing a Knight on any field of a chessboard of any size $x*y$. Then finding a path on said chessboard where the Knight visits every field exactly one time.
Visualization
//put in drawings
Constrains
- Only looking at boards that are cubes: $x=y:x^2$.
- We want a board where a field is visited has the corresponding move nubmer it was visited in.
The following expression describes our solved board:
$\forall x,y \in \mathbb{N}| 0 \leq x = y < length: board(x,y) \in \{1,2,\dots,lenght^2\}$
the length is the length of ether side of the board
First implementation
Mise en place
We need a simple field and initialize our board as a number matrix like the following:
interface Field {
x: number;
y: number;
}
const board: number[][] = [];
const rows: number = 6;
const cols: number = 6;
for (let i: number = 0; i < rows; i++) {
board[i] = [];
for (let j: number = 0; j < cols; j++) {
board[i][j] = 0;
}
}
And calling our logic entrypoint facade:
const found = solveForKnight(board, { x: 1, y: 0 } as Field);
console.table(board);
console.log("Found?", found);
Which looks like the following:
function solveForKnight(board: number[][], startField: Field): boolean {
const found: boolean = findKnightPath(board, startField, 1);
return found;
}
I personally like this approach because the user of this algorythm does and should not care how the algorythm itself is called/initialized.
The logic itself
The solver function itself
function findKnightPath(board: number[][], tryField: Field, level: number): boolean {
}
One of the pillers of this algorythm is the base condition. At what state do we have a solution.
if (level == board[0].length * board.length) {
board[tryField.y][tryField.x] = level;
return true;
} else{
// ...
}
We know that we found a path when we are on the last, unvisited, field of the board.
If we are currently not working with the last field, we need to continiue.
else {
board[tryField.y][tryField.x] = level;
let found: boolean = false;
let move: number = 0;
while (!found && move < 8) {
const newField: Field | null = nextMoveKnight(board, tryField, move);
if (newField != null && board[newField.y][newField.x] == 0) {
found = findKnightPath(board, newField, level + 1);
}
move++;
}
if (!found) {
board[tryField.y][tryField.x] = 0;
}
return found;
}
Now is a great time to talk about the actual progression. How can the knight move over the board and what are all of its possible moves. In the following drawing the knight is represented as a "circle" and its possible next positions marked as with an "x".
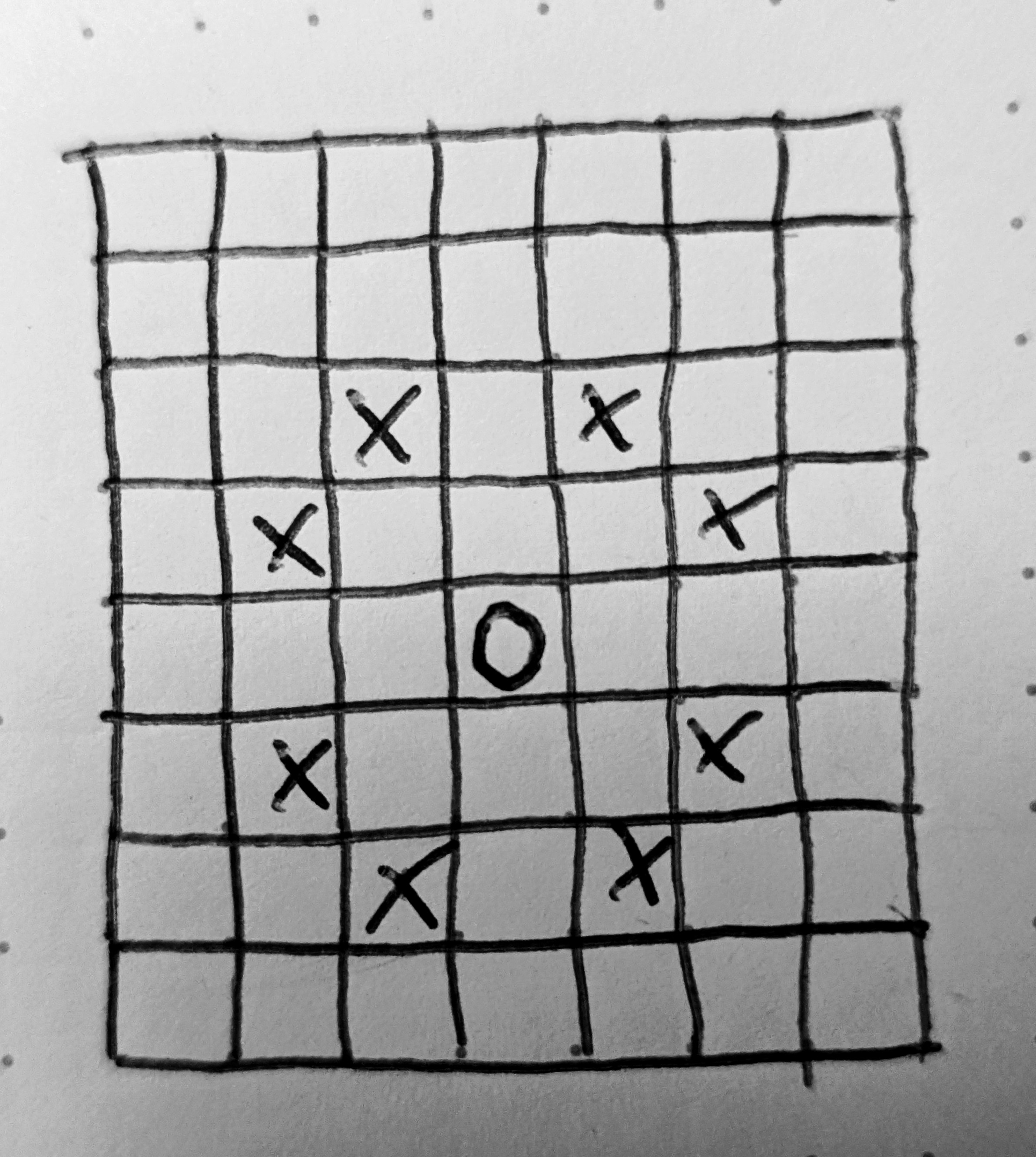
Note that we will also need to handle positions that are invalid to the knights relative position. For example, the knight standing on the edge of the board.
To calculate the next position of the knight i naivly used the following implementation:
function nextMoveKnight(board: number[][], currentField: Field, move: number): Field | null {
const x: number = currentField.x;
const y: number = currentField.y;
let newX: number | null = -1;
let newY: number | null = -1;
if (move == 0) {
newX = x - 1;
newY = y - 2;
} else if (move == 1) {
newX = x + 1;
newY = y - 2;
} else if (move == 2) {
newX = x + 2;
newY = y - 1;
} else if (move == 3) {
newX = x + 2;
newY = y + 1;
} else if (move == 4) {
newX = x + 1;
newY = y + 2;
} else if (move == 5) {
newX = x - 1;
newY = y + 2;
} else if (move == 6) {
newX = x - 2;
newY = y + 1;
} else if (move == 7) {
newX = x - 2;
newY = y - 1;
}
if (0 <= newX && 0 <= newY && newX < board[0].length && newY < board.length) {
return { x: newX, y: newY } as Field;
}
return null;
}
And the algorythm handles/skipes invalid fields represented by a null value.
Checkpoint 1
It works! But only for boards with the size up to $6^2$ and only depending on the knights starting position. (on my old laptop)
Using the start field $x = 1, y = 0$
> node --experimental-transform-types main.ts
┌─────────┬────┬────┬────┬────┬────┬────┐
│ (index) │ 0 │ 1 │ 2 │ 3 │ 4 │ 5 │
├─────────┼────┼────┼────┼────┼────┼────┤
│ 0 │ 36 │ 1 │ 30 │ 5 │ 20 │ 3 │
│ 1 │ 31 │ 28 │ 19 │ 2 │ 11 │ 6 │
│ 2 │ 18 │ 35 │ 10 │ 29 │ 4 │ 21 │
│ 3 │ 27 │ 32 │ 25 │ 14 │ 7 │ 12 │
│ 4 │ 24 │ 17 │ 34 │ 9 │ 22 │ 15 │
│ 5 │ 33 │ 26 │ 23 │ 16 │ 13 │ 8 │
└─────────┴────┴────┴────┴────┴────┴────┘
Found? true
Optimizing possible next moves
An idea is to not let the knight move to the next free field. But to sort these fields by specific properties. For exampe: try the next move, that itself has the least possible next moves. Letting the knight move around the edges of the board, trying all fields and then moving in.
The main recursion/backtracking changes. From getting each move to getting a list of moves at once an trying them:
const moves: Field[] = nextKnightMoves(board, tryField);
let index: number = 0;
while (!found && index < moves.length) {
found = findKnightPath(board, moves[index], level + 1);
index++;
}
The nextKnightMoves handles the logic of getting the next moves and evaluating each of the moves for their probability. A fancy word for this use case.
- we get the next possible moves of the current position
- iterate over them and count how many possible move each of them has
- sort them by that number and give back the fields
function nextKnightMoves(board: number[][], currentField: Field): Field[] {
let possibleMoves: PossibleMove[] = nextMovesFromCurrentPosition(board, currentField);
let index: number = 0;
while (index < possibleMoves.length) {
const possibleMove: Field = possibleMoves[index].field;
board[possibleMove.y][possibleMove.x] = 1; // set it to any value to be "visited"
possibleMoves[index].moveCount = nextMovesFromCurrentPosition(board, possibleMoves[index].field).length;
board[possibleMove.y][possibleMove.x] = 0;
index++;
}
//sort by moveCount
possibleMoves = possibleMoves.sort((a, b) => {
if (a.moveCount == b.moveCount) {
return 0;
}
return a.moveCount > b.moveCount ? 1 : -1;
});
return possibleMoves.map(possibleMove => possibleMove.field);
}
You will notice that we used the new type PossibleMove for this to track the moveCount of each possible move.
interface PossibleMove {
moveCount: number;
field: Field;
}
I also took the chance to "simplefy" the larger if else statement to get the next possible moves
function nextMovesFromCurrentPosition(board: number[][], currentField: Field): PossibleMove[] {
let nextMoves: PossibleMove[] = [];
const xMovement: number[] = [-1, 1, 2, 2, 1, -1, -2, -2];
const yMovement: number[] = [-2, -2, -1, +1, +2, +2, +1, -1];
let index: number = 0;
while (index < xMovement.length) {
const x: number = currentField.x + xMovement[index];
const y: number = currentField.y + yMovement[index];
if (0 <= x && 0 <= y && x < board[0].length && y < board.length) {
if (board[y][x] == 0) {
nextMoves.push({ "moveCount": 0, "field": { x: x, y: y } as Field });
}
}
index++;
}
return nextMoves;
}
- The knights move logic is known, so we can extract this logic into two array and simple arithmetic.
- Also checking if each move is legal (on the board) and not already visited
Know we can also solve for boards that are for example $20^2$. Also starting at $x=1, y=0$
┌─────────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┐
│ (index) │ 0 │ 1 │ 2 │ 3 │ 4 │ 5 │ 6 │ 7 │ 8 │ 9 │ 10 │ 11 │ 12 │ 13 │ 14 │ 15 │ 16 │ 17 │ 18 │ 19 │
├─────────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┤
│ 0 │ 4 │ 1 │ 6 │ 59 │ 80 │ 63 │ 40 │ 75 │ 82 │ 173 │ 38 │ 165 │ 84 │ 103 │ 36 │ 95 │ 86 │ 91 │ 34 │ 93 │
│ 1 │ 7 │ 58 │ 3 │ 64 │ 41 │ 76 │ 81 │ 284 │ 39 │ 166 │ 83 │ 174 │ 37 │ 150 │ 85 │ 102 │ 35 │ 94 │ 87 │ 90 │
│ 2 │ 2 │ 5 │ 60 │ 79 │ 62 │ 283 │ 74 │ 167 │ 326 │ 285 │ 172 │ 149 │ 164 │ 101 │ 104 │ 147 │ 96 │ 89 │ 92 │ 33 │
│ 3 │ 57 │ 8 │ 65 │ 42 │ 77 │ 168 │ 333 │ 286 │ 303 │ 170 │ 325 │ 162 │ 175 │ 148 │ 151 │ 100 │ 105 │ 130 │ 97 │ 88 │
│ 4 │ 46 │ 43 │ 78 │ 61 │ 282 │ 73 │ 302 │ 169 │ 334 │ 327 │ 304 │ 171 │ 152 │ 163 │ 154 │ 139 │ 146 │ 99 │ 32 │ 107 │
│ 5 │ 9 │ 56 │ 45 │ 66 │ 53 │ 332 │ 287 │ 348 │ 329 │ 340 │ 335 │ 324 │ 161 │ 176 │ 145 │ 126 │ 131 │ 106 │ 129 │ 98 │
│ 6 │ 44 │ 47 │ 54 │ 281 │ 72 │ 301 │ 330 │ 339 │ 342 │ 349 │ 328 │ 305 │ 318 │ 153 │ 140 │ 155 │ 138 │ 127 │ 108 │ 31 │
│ 7 │ 55 │ 10 │ 67 │ 52 │ 331 │ 288 │ 353 │ 358 │ 347 │ 338 │ 341 │ 336 │ 323 │ 160 │ 177 │ 144 │ 125 │ 132 │ 123 │ 128 │
│ 8 │ 48 │ 51 │ 280 │ 71 │ 300 │ 367 │ 356 │ 345 │ 352 │ 343 │ 350 │ 317 │ 306 │ 319 │ 196 │ 141 │ 156 │ 137 │ 30 │ 109 │
│ 9 │ 11 │ 68 │ 49 │ 376 │ 289 │ 354 │ 359 │ 366 │ 357 │ 346 │ 337 │ 322 │ 249 │ 230 │ 159 │ 178 │ 143 │ 124 │ 133 │ 122 │
│ 10 │ 50 │ 279 │ 70 │ 299 │ 378 │ 373 │ 368 │ 355 │ 344 │ 351 │ 316 │ 307 │ 320 │ 197 │ 142 │ 195 │ 136 │ 157 │ 110 │ 29 │
│ 11 │ 69 │ 12 │ 377 │ 290 │ 375 │ 360 │ 379 │ 372 │ 365 │ 370 │ 321 │ 250 │ 229 │ 248 │ 231 │ 158 │ 179 │ 186 │ 121 │ 134 │
│ 12 │ 278 │ 291 │ 298 │ 383 │ 380 │ 395 │ 374 │ 369 │ 362 │ 313 │ 308 │ 315 │ 252 │ 227 │ 198 │ 225 │ 194 │ 135 │ 28 │ 111 │
│ 13 │ 13 │ 382 │ 293 │ 394 │ 297 │ 384 │ 361 │ 386 │ 371 │ 364 │ 251 │ 228 │ 247 │ 232 │ 241 │ 182 │ 187 │ 180 │ 185 │ 120 │
│ 14 │ 292 │ 277 │ 296 │ 381 │ 398 │ 391 │ 396 │ 363 │ 312 │ 309 │ 314 │ 253 │ 242 │ 199 │ 226 │ 193 │ 224 │ 183 │ 112 │ 27 │
│ 15 │ 275 │ 14 │ 399 │ 294 │ 393 │ 270 │ 385 │ 310 │ 387 │ 254 │ 243 │ 246 │ 217 │ 240 │ 233 │ 236 │ 181 │ 188 │ 119 │ 184 │
│ 16 │ 264 │ 295 │ 276 │ 271 │ 390 │ 397 │ 392 │ 255 │ 244 │ 311 │ 216 │ 239 │ 234 │ 237 │ 200 │ 223 │ 192 │ 221 │ 26 │ 113 │
│ 17 │ 15 │ 274 │ 265 │ 400 │ 261 │ 258 │ 269 │ 388 │ 215 │ 210 │ 245 │ 212 │ 205 │ 218 │ 235 │ 220 │ 201 │ 116 │ 189 │ 118 │
│ 18 │ 266 │ 263 │ 272 │ 17 │ 268 │ 389 │ 260 │ 19 │ 256 │ 213 │ 208 │ 21 │ 238 │ 203 │ 206 │ 23 │ 222 │ 191 │ 114 │ 25 │
│ 19 │ 273 │ 16 │ 267 │ 262 │ 259 │ 18 │ 257 │ 214 │ 209 │ 20 │ 211 │ 204 │ 207 │ 22 │ 219 │ 202 │ 115 │ 24 │ 117 │ 190 │
└─────────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┘
Found? true
Or starting at $x=10, y=10$ and watching the knight naturally walk back to the edges. (i really enjoyed myself trying different output variations)
┌─────────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┐
│ (index) │ 0 │ 1 │ 2 │ 3 │ 4 │ 5 │ 6 │ 7 │ 8 │ 9 │ 10 │ 11 │ 12 │ 13 │ 14 │ 15 │ 16 │ 17 │ 18 │ 19 │
├─────────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┤
│ 0 │ 43 │ 40 │ 131 │ 134 │ 45 │ 6 │ 127 │ 144 │ 47 │ 8 │ 123 │ 118 │ 49 │ 10 │ 111 │ 102 │ 51 │ 12 │ 55 │ 98 │
│ 1 │ 132 │ 135 │ 44 │ 41 │ 130 │ 143 │ 46 │ 7 │ 126 │ 177 │ 48 │ 9 │ 122 │ 117 │ 50 │ 11 │ 96 │ 99 │ 52 │ 13 │
│ 2 │ 39 │ 42 │ 133 │ 142 │ 181 │ 128 │ 5 │ 178 │ 145 │ 124 │ 147 │ 166 │ 119 │ 110 │ 101 │ 112 │ 103 │ 54 │ 97 │ 56 │
│ 3 │ 136 │ 141 │ 182 │ 129 │ 198 │ 179 │ 186 │ 125 │ 192 │ 167 │ 176 │ 121 │ 148 │ 157 │ 116 │ 109 │ 100 │ 95 │ 14 │ 53 │
│ 4 │ 183 │ 38 │ 199 │ 180 │ 185 │ 190 │ 197 │ 4 │ 187 │ 146 │ 193 │ 156 │ 165 │ 120 │ 149 │ 106 │ 113 │ 104 │ 57 │ 90 │
│ 5 │ 140 │ 137 │ 184 │ 295 │ 200 │ 307 │ 188 │ 191 │ 196 │ 203 │ 168 │ 175 │ 172 │ 155 │ 158 │ 115 │ 108 │ 89 │ 94 │ 15 │
│ 6 │ 37 │ 298 │ 139 │ 308 │ 189 │ 296 │ 201 │ 306 │ 3 │ 194 │ 173 │ 204 │ 169 │ 164 │ 107 │ 150 │ 105 │ 114 │ 91 │ 58 │
│ 7 │ 138 │ 301 │ 294 │ 297 │ 320 │ 305 │ 310 │ 195 │ 202 │ 219 │ 232 │ 171 │ 174 │ 205 │ 154 │ 159 │ 88 │ 151 │ 16 │ 93 │
│ 8 │ 299 │ 36 │ 321 │ 304 │ 309 │ 328 │ 319 │ 338 │ 311 │ 2 │ 217 │ 220 │ 233 │ 170 │ 163 │ 206 │ 153 │ 92 │ 59 │ 84 │
│ 9 │ 302 │ 293 │ 300 │ 327 │ 322 │ 339 │ 376 │ 329 │ 218 │ 337 │ 312 │ 231 │ 216 │ 221 │ 234 │ 87 │ 160 │ 85 │ 152 │ 17 │
│ 10 │ 35 │ 324 │ 303 │ 340 │ 375 │ 364 │ 345 │ 318 │ 377 │ 330 │ 1 │ 244 │ 271 │ 236 │ 215 │ 162 │ 207 │ 78 │ 83 │ 60 │
│ 11 │ 292 │ 341 │ 326 │ 323 │ 344 │ 381 │ 388 │ 365 │ 346 │ 317 │ 336 │ 313 │ 230 │ 243 │ 222 │ 235 │ 86 │ 161 │ 18 │ 77 │
│ 12 │ 325 │ 34 │ 343 │ 386 │ 395 │ 374 │ 363 │ 380 │ 335 │ 378 │ 331 │ 272 │ 245 │ 270 │ 237 │ 214 │ 79 │ 208 │ 61 │ 82 │
│ 13 │ 342 │ 291 │ 394 │ 371 │ 384 │ 387 │ 382 │ 389 │ 366 │ 347 │ 316 │ 269 │ 314 │ 229 │ 242 │ 223 │ 238 │ 81 │ 76 │ 19 │
│ 14 │ 33 │ 356 │ 385 │ 396 │ 391 │ 398 │ 373 │ 362 │ 379 │ 334 │ 349 │ 332 │ 273 │ 246 │ 267 │ 80 │ 213 │ 74 │ 209 │ 62 │
│ 15 │ 290 │ 393 │ 370 │ 399 │ 372 │ 383 │ 390 │ 367 │ 348 │ 361 │ 260 │ 315 │ 268 │ 275 │ 228 │ 241 │ 224 │ 239 │ 20 │ 75 │
│ 16 │ 355 │ 32 │ 357 │ 392 │ 397 │ 368 │ 359 │ 280 │ 259 │ 350 │ 333 │ 274 │ 251 │ 266 │ 247 │ 264 │ 73 │ 212 │ 63 │ 210 │
│ 17 │ 286 │ 289 │ 400 │ 369 │ 358 │ 283 │ 256 │ 351 │ 360 │ 279 │ 250 │ 261 │ 276 │ 263 │ 70 │ 227 │ 240 │ 225 │ 66 │ 21 │
│ 18 │ 31 │ 354 │ 287 │ 284 │ 29 │ 352 │ 281 │ 254 │ 27 │ 258 │ 277 │ 252 │ 25 │ 248 │ 265 │ 72 │ 23 │ 68 │ 211 │ 64 │
│ 19 │ 288 │ 285 │ 30 │ 353 │ 282 │ 255 │ 28 │ 257 │ 278 │ 253 │ 26 │ 249 │ 262 │ 71 │ 24 │ 69 │ 226 │ 65 │ 22 │ 67 │
└─────────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┘
Found? true
One of my first articles. Lets see how long this will hold on for.